Join the Financial Terms Telegram channel and get a new financial term every day.
I created an app for this project that generates the terms and definitions in my style, turns them into an image, and posts it in Telegram at the specified time.
If the mortgage rate is high, more people would prefer renting apartments instead of buying a house. That drives rent prices up. The problem is that due to the high inflation, the price of a house also rises.
The price for housing also rises when the mortgage rate is low. Then it is much easier to take 30-year long mortgage and get your own housing instead of paying expensive rent and getting nothing at the end of the rent term. Then more people will buy a house with a mortgage. With higher demand comes higher price. So the price for housing rises.
In some countries, government incentivises taking a mortgage. Military servants usually get lower mortgage rates. In UK if a person above 18 buys his first house for less than 500k$, he pays only half of a house price. In Netherlands, government insures mortgages, meaning, if a person is insolvent to pay for a mortgage, government will buy a house from a bank, and return money from mortgage payments to a person. The government will also give a discounted rent for a person (I will check this information, I can be mistaken). Therefore the prices for a condo in Amsterdam tripled (if i don’t mistaken). All of these incentives drive prices for housing up.
Real estate market has a huge problem – it is hard for prices to fall. Not only because of scarcity of land, higher price for materials and labor costs. There are no market mechanisms to make prices fall. In the stock market, it is possible to short stocks – sell the stock that you don’t own, and buy it back when price falls, making the profit in the difference. Short selling works with stocks, because the stocks of one company are identical, their value is always the same.
It is not possible to find 2 exactly the same houses, even Soviet flats have different views, neighbors, and house condition. Therefore, short is not really possible.
To lower the housing price, either the place should loose the attractiveness or the new technologies should make housing cheaper. That what happens in the US market. New housing for the mid-class household became simplier and smaller than before. Remember the housing in Manhattan and Brooklyn of 20th century – the red brick houses with fire stairways on the façade. Compare their quality and design with new housing: the cheap coloured ventilated panels with studio apartments.
The example of attractiveness loss was on 9/11. Based on the Federal Reserve Bank of New York, most of the employees who worked nearby moved to other parts of New York City or New Jersey. The rent prices for an office in Manhattan dropped from 52.5$ to 50.75$ per square foot. By November 2001, 57 million square feet near Trade Center were traded on market just for 41.81$ (Pearson, Macroeconomics, page 54). but that happened with offices. What about the households?
More people started to buy one-family houses near New York. The prices went up 10-15% comparing with previous year. Even thought, the average price of one-family house in the US has fallen.
After looking at the graph, we see that there was only one fall of housing in the Mortgage crisis of 2008-2009. The crisis basically happened, because banks gave too much mortgages to people, who had a huge risk to become insolvent.
Thousands of people couldn’t pay off the debts. Their houses were put for a sale. The supply of houses was so high, that the prices went down. Construction companies stopped building houses, just because there were not too much people who could afford houses and not so much banks would give mortgages. For construction companies it is very bad – they should sell nearly 70% of housing as fast as possible to pay off the debts. Therefore, a lot of companies became bankrupt and ceased the construction of objects.
Such situation lasts till the supply is covered by demand. Meaning that prices fall to a fair price. When it is happened, the construction continues.
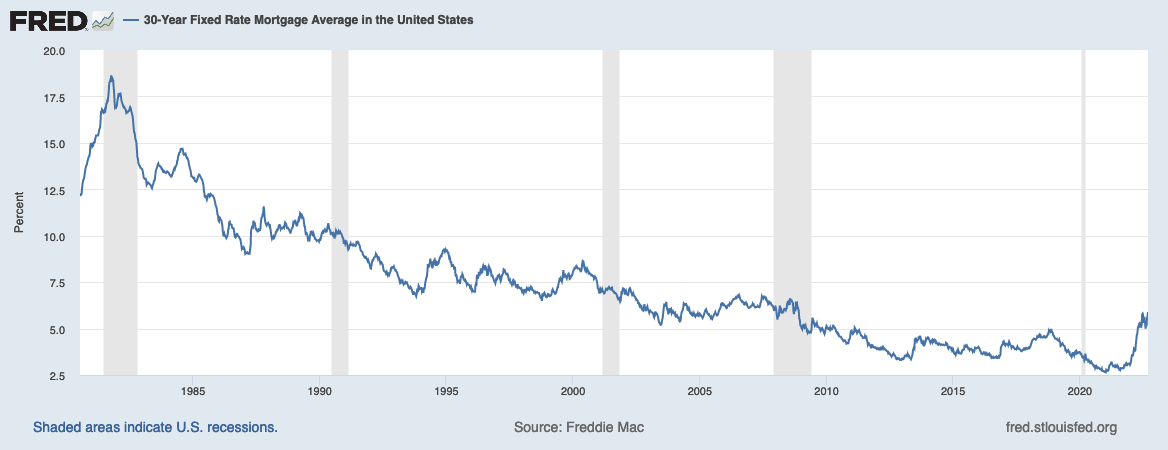
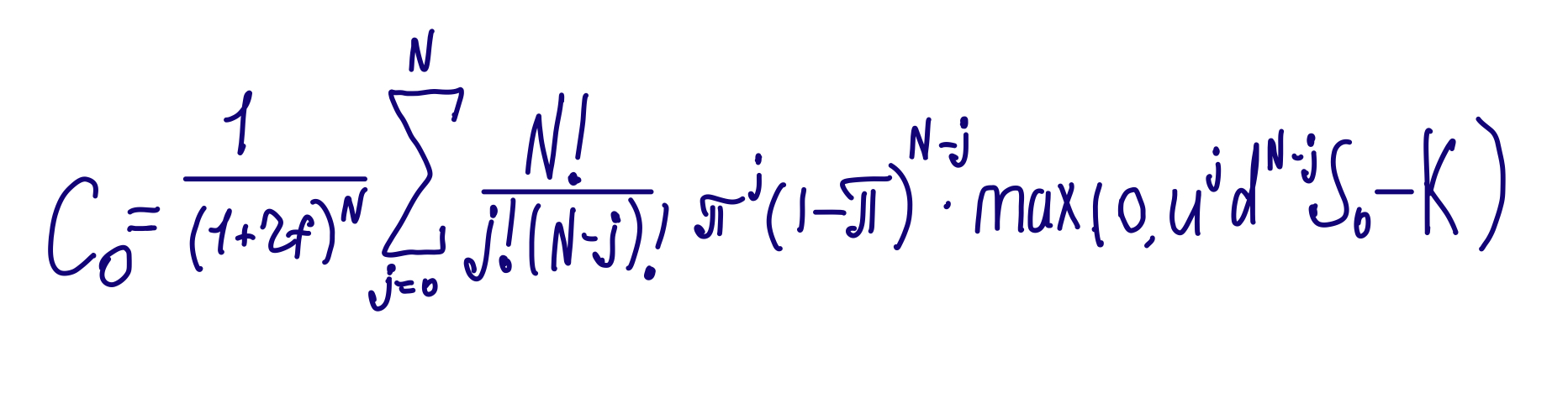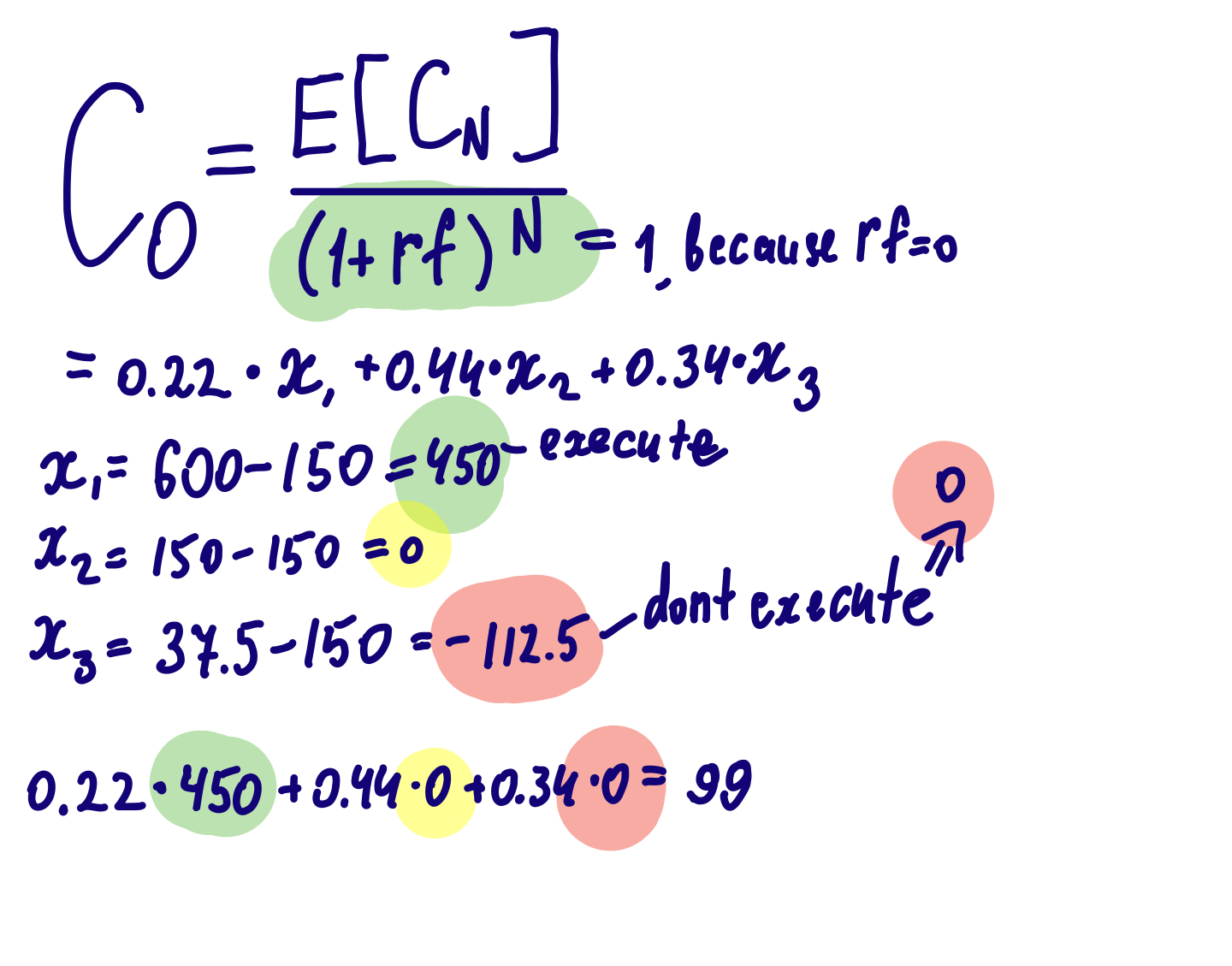An option is a paper, that gives you a right (not duty) to buy stocks (or anything else) on a specific day. For example, you bought an option for 5$ which gives you the right to buy 1 share of Apple in one year for today’s price of 150$. You expect Apple stocks to rise by more than 5$. Let’s see 3 scenarios of Apple price in one year:
170$, we realize the option and get a profit of 170-150-5 = 15$. This is a 200% return. If we invested in a share, we would have got 170-150 = 20$ profit, 13%.
130$, we don’t realize an option, because now the shares cost less, than in the contract (150$). We lose 5$ (the cost of an option) instead of 130-150=-20$ if we bought a share.
150$-155$, we may realize an option and get a small loss. 153-150-5=-2$. We lost 40$ instead of 2% profit.
If we had bought the shares, we would have risked losing all the share costs. Here we risk losing only the option price of 5$.
A seller wants to have a profit from a share. Instead of thinking about whether the stock price will be as high as he wants or not, he can just say: “I want to get 20$ profit in one year from Apple shares that cost 150$, everything that is higher is yours”. To do so, he sells the option for 20$. A seller immediately gets a profit of 20$ and can invest then in something else. Even if the share price drops by 20$ to 130$, he does not lose anything, as well as a buyer.
Companies also issue options – Warrants. Companies give premiums to employees as an option for buying a share of a company. For example, Elon Musk gives Tesla employees options for buying tesla at a huge discount, that they can realize at any time. So that when employees save enough, they can invest money in a company. It is an alternative to convertible bonds.
European call (put)option is the right to buy(sell) a unit of an underlying asset at a strike (=pre-specified) price at a specific point in time.
American call (put)option is the right to buy(sell) a unit of an underlying asset at any time on or before an expiration date of an option. European options can also be without an expiration date.
American options are also traded in Europe, in the Netherlands stock exchange, Euronext.liffe, for example. These options are traded primarily on equities: FTSE-100, CAC40, Bel-20.
It is hard to estimate the price of an option. There are parameters, such as risk-free rate, time to expiration, and volatility (variance, or price fluctuation). For example, low-volatility options cost less over time, while high-volatility options cost a lot.
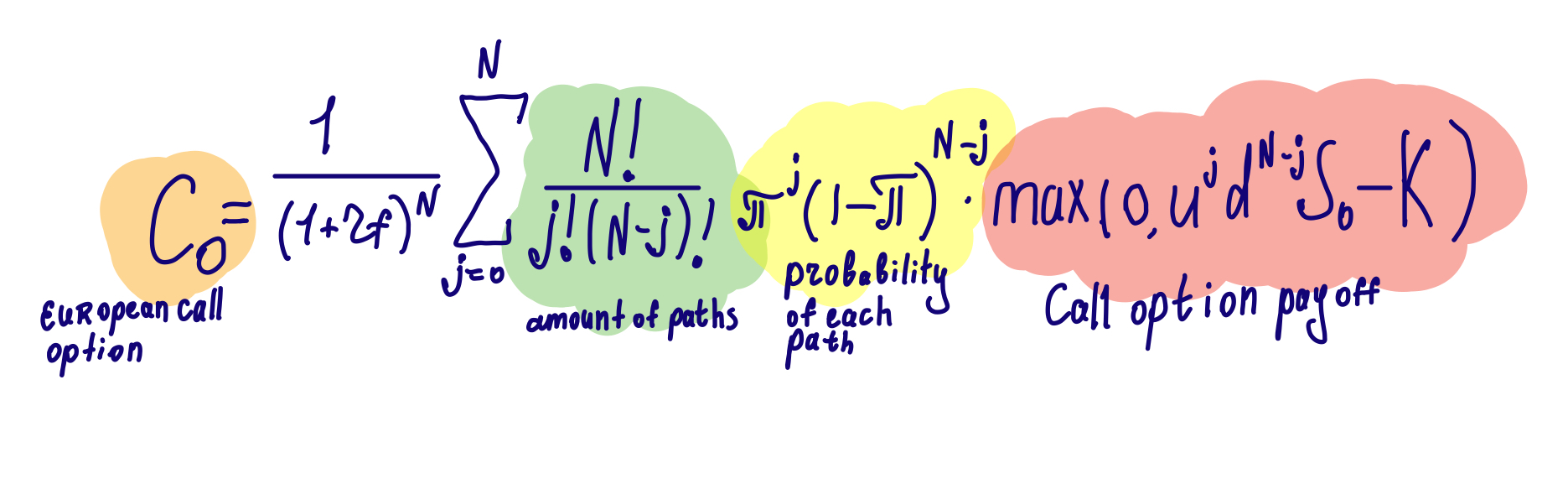
Binomial formula for pricing European options.
Let’s understand each part of the equation:
The U and D are the possible outcomes (in $) of events. We assume, that there are always two scenarios in one period of time: positive and negative. Some traders use 1 second as a period, but then in 1 minute, there are 2^60, more than 1 billion scenarios. We assume 1 period as a quarter, half, or a full year.
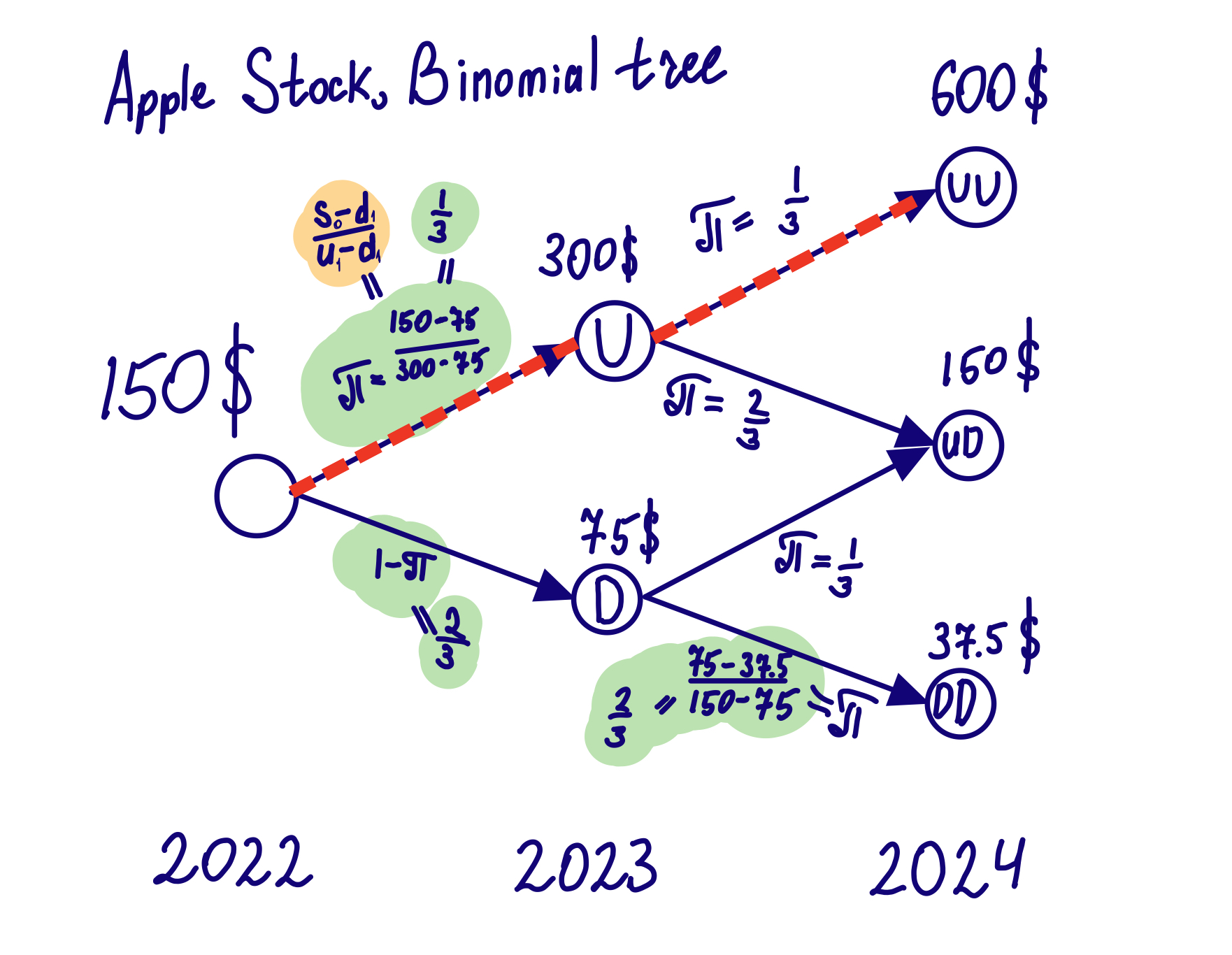
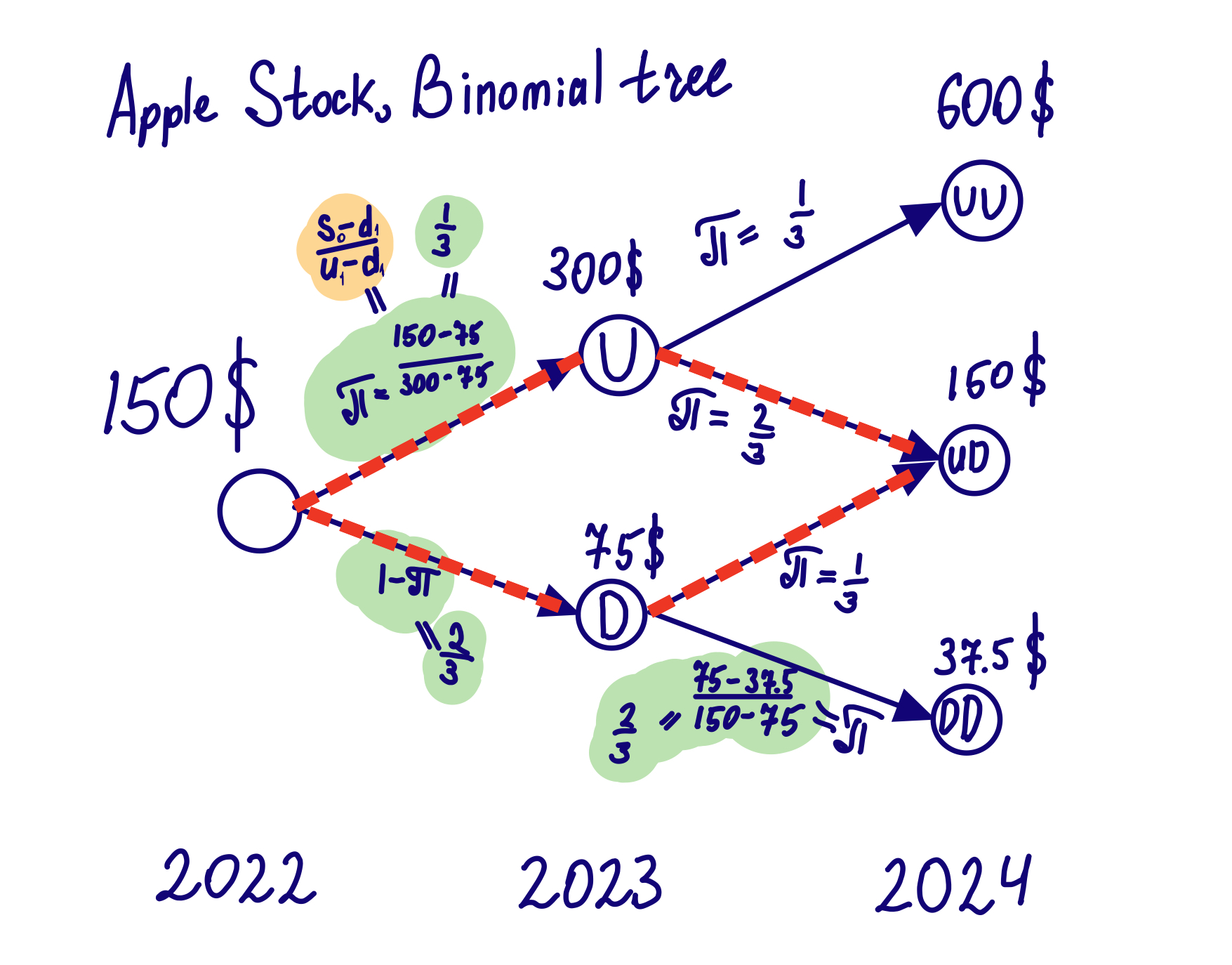
We put all possible outcomes in a binomial tree – a graph, with 2 inherited sub-elements on each node. Let’s see the binomial tree example of Apple stock, which can either double or halve, and we also assume, that the risk-free rate is equal to 0 for simplicity:
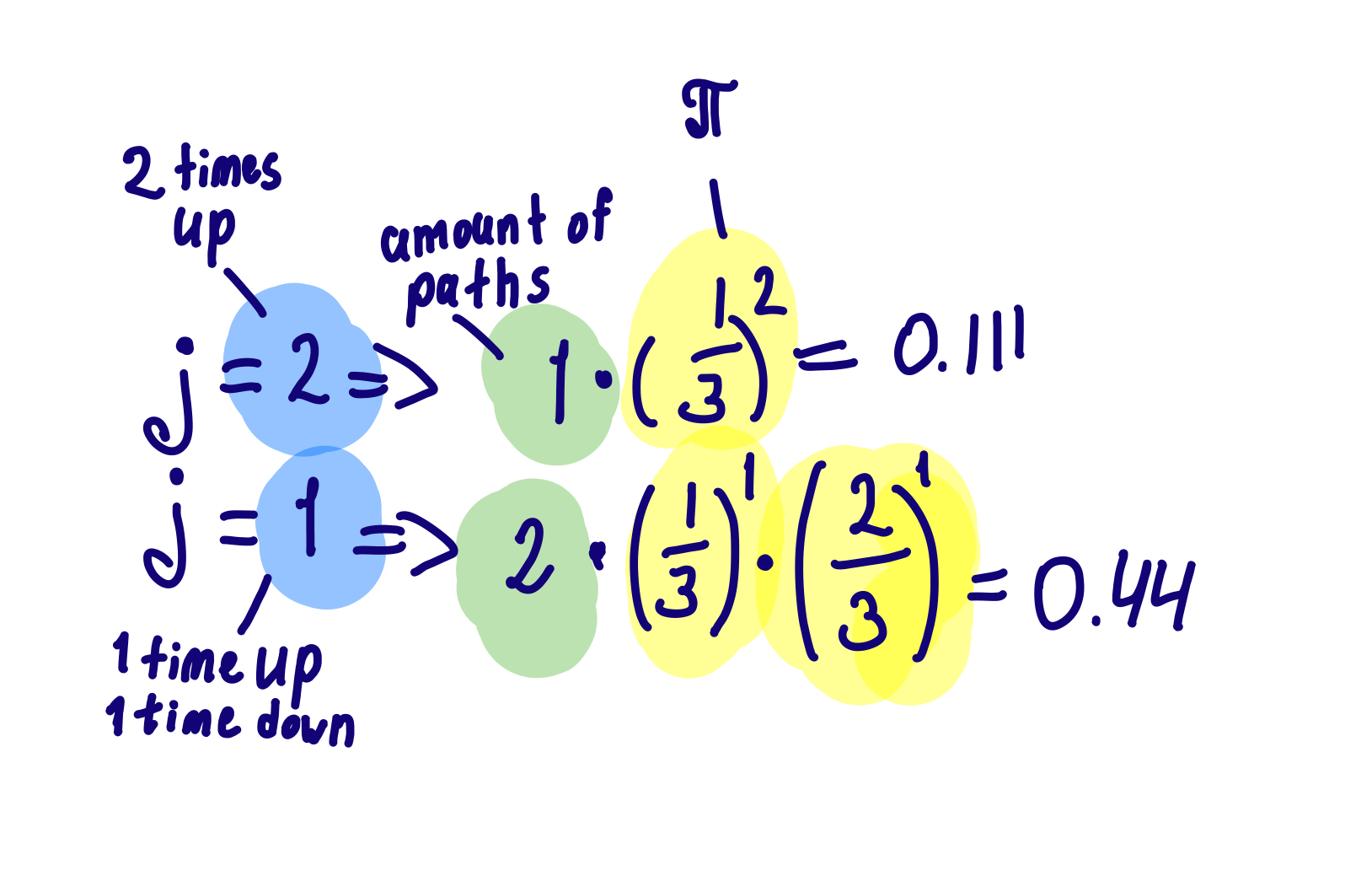
now we count the path to each final node:
It is 1 to UU, 2 to UD, and 1 to DD. Now we find the probability of each of the nodes.
The probability of the last one is 1 – 0.22 – 0.44 = 0.34. Yes, the probability of the nodes is neither 25% nor 33%, it is not similarly distributed. It can only be similarly distributed if π=0.5
Finally, we find the option price. We will assume that we need the strike price at the moment (ATM), that is equal to the spot value (S0):
The option price is equal to 99$.
Black Sholes Formula for American and European Options, with no-arbitrage:
arbitrage is a risk-free profit, that happens when tracking a portfolio (or a share) costs more (or less) than the derivative (forward or an option). If the share price is higher than the forward strike price (end-price) + the cost of a forward, then we short the share and buy a forward or an option.
That means if an Apple share costs 160$ and the forward cost is 0$, and the strike price is 150$, then we short apple stock and buy forwards. We get 160-150=10$ profit. Moreover, when we short a stock, we get the cost of a share to our account, that we can put in a bank. That brings a lot of profit.
Let’s use an option in the example above. Let’s assume that an option is free. We have the same profit if the cost of apple stock is higher than 150$. If apple costs less than 150$, we just don’t exercise the option and get profit from shorting a stock. If the cost of an option was 10$, then we just have a profit of 160-150-5 + 160*(risk-free rate, such as a bank deposit).
As a result, we get risk-free profit from such operations. In a world with unlimited buyers and sellers, we could do the operation over and over again and become the richest people immediately, or in the end of a period.
Put-Call parity Price of a call (buy) and put (sell) options is different. that is because of a risk-free rate. We use an equation:
Call price - Put price = Current price - Present value of a Strike price
Call price - Put price = Current price - Strike price / (1 + risk-free rate)^periods
# usually, a period is equal to 1 year and is named "t"
C0 - P0 = S0 - K/(1 + rf)^tDue to the always non-negative risk-free rate (because otherwise, you don’t put money in the bank account), the price of a call is higher than the put.